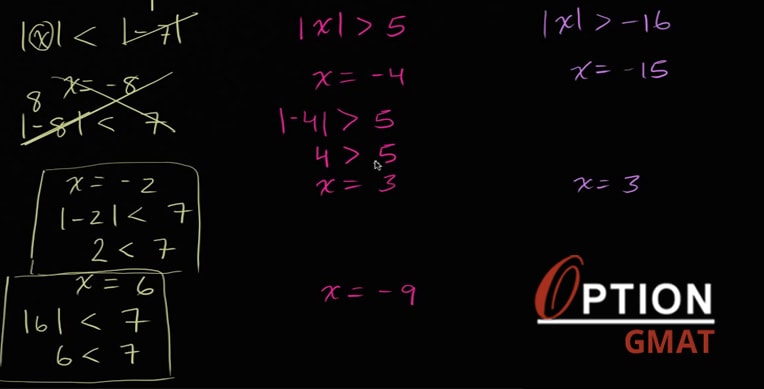- Have any questions?
- +971 509267126
- +971 551207626
- enquiry@optioneducation.ae
Absolute Values and Inequalities
An Illusion!
July 29, 2016
GMAT Probability
November 2, 2016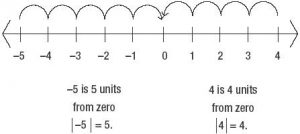
Absolute values
The absolute value represents the distance from zero on a number line. Mathematically absolute of X is written as |X|. Absolute value is always positive because it disregards the direction (whether negative or positive). For example, the number 7 is exactly 7units away from 0, so the absolute value of 7 equals 7 (i.e.|7|=7). To find the absolute value of -7, look at the real number line, number -7 is also exactly 7 units away from 0 (i.e.|-7|=7). In general
|positive| = positive
|negative| = positive
Absolute value bars (i.e.| |) are conceptually a measure of the distance of the expression inside the bar from zero.
Solving Equations with Absolute Values:
An equation with an absolute value has two solutions and it is solved by considering two circumstances.
Example: |2x-4|>6
1. Write the problem without absolute sign and solve the inequalities.
2x-4>6
2x > 10
x >5
2. Write the problem without absolute value sign, reverse the inequality and negate the value not under absolute value and solve the inequalities.
2x-4 < -6
2x<-6+4
2x<-2
x<-1
The interval notation for this solution is -1>x>5. Multiplying inequality range by negative, inequality signs are reversed and this can also be written as 1<x<-5.
Inequalities
A mathematical statement that uses one of the following inequality signs is called an inequality.
< Less than
> Greater than
≤ Less than or equal to
≥ Greater than or equal to
Inequalities can involve variables and are similar to equations, except that the two sides are related by one of the inequality signs instead of the equality sign used in equations.
The procedure used to solve a linear inequality is similar to that used to solve a linear equation, which is to simplify the inequality by isolating the variable on one side of the inequality, using the following two rules.
Rule 1: When the same constant is added to or subtracted from both sides of an inequality, the direction of the inequality is preserved and the new inequality is equivalent to the original.
Example:
-5 ≤ A < 6
-5+2 ≤ A < 6+2
-3 ≤ A <8
Rule 2: When both sides of the inequality are multiplied or divided by the same nonzero constant, the direction of the inequality is preserved if the constant is positive but the direction is reversed if the constant is negative. In either case, the new inequality is equivalent to the original.
Example:
-5 ≤ A < 6
Multiply the above inequality by -2 on the both sides
-2 x -5 ≤ A < 6 x -2
-12<A ≤ 10
51 Comments
My brother recommended I might like this web site He was totally right This post actually made my day You cannt imagine just how much time I had spent for this information Thanks
Hi i think that i saw you visited my web site thus i came to Return the favore Im attempting to find things to enhance my siteI suppose its ok to use a few of your ideas
QVokndurblH
I couldn’t help but be enthralled with the basic information you offered about your visitors, so much so that I returned to your website to review and double-check recently published content.
lipitor 20mg oral cheap lipitor 80mg buy lipitor 40mg
order baycip pills – brand cipro 1000mg amoxiclav over the counter
ciprofloxacin 1000mg without prescription – how to get clavulanate without a prescription augmentin 625mg usa
I’ve been surfing on-line greater than three hours as of
late, yet I by no means found any interesting article like yours.
It’s lovely worth sufficient for me. Personally, if all web owners and bloggers made good content as you
did, the internet shall be a lot more helpful than ever before.
Wow, amazing weblog format! How lengthy have you ever been running a blog for?
you made blogging look easy. The whole glance of your website
is magnificent, let alone the content material! You can see similar here sklep internetowy
purchase metronidazole online – buy cheap generic cefaclor zithromax online
ciplox for sale – amoxicillin uk
erythromycin 500mg pill
valor do tadalafil tadalafil citrate erfahrung cialis increase testosterone
helloI like your writing very so much proportion we keep up a correspondence extra approximately your post on AOL I need an expert in this space to unravel my problem May be that is you Taking a look forward to see you
buy generic valtrex over the counter – vermox 100mg without prescription zovirax 800mg usa
stromectol 3mg – how to buy ciplox buy generic tetracycline for sale
buy flagyl online cheap – buy oxytetracycline 250mg pills buy zithromax 250mg generic
oral acillin ampicillin buy online where can i buy amoxicillin
I’m gone to convey my little brother, that he should also visit this weblog on regular
basis to get updated from most recent news update. I saw similar here:
Dobry sklep
lasix 40mg pill – warfarin 2mg cost order captopril 25 mg online cheap
mexican cialis name taking cialis daily cialis tadalafil generika
Howdy! Do you know if they make any plugins to assist with
Search Engine Optimization? I’m trying to get my blog to rank for some
targeted keywords but I’m not seeing very good success.
If you know of any please share. Many thanks! You can read similar blog here: Sklep internetowy
It’s very interesting! If you need help, look here: ARA Agency
order metformin 500mg online – order glycomet 1000mg online cheap how to get lincomycin without a prescription
buy cheap generic zidovudine – purchase allopurinol without prescription
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me.
sildenafil citrate wikipedia sildenafil medicine names sildenafil visual disturbances
quetiapine oral – purchase luvox without prescription cheap generic eskalith
buy clomipramine for sale – cymbalta pill doxepin for sale online
hydroxyzine 25mg usa – order buspirone 10mg online amitriptyline drug
sildenafil daily dosage sildenafil citrate avis viagra falls address
cheap amoxil sale – buy amoxil sale cipro over the counter
Hi! Do you know if they make any plugins to assist with Search Engine Optimization? I’m trying to get
my site to rank for some targeted keywords but I’m not seeing very good results.
If you know of any please share. Cheers! You can read similar article here:
Backlinks List
I have been surfing online more than 3 hours today yet I never found any interesting article like yours It is pretty worth enough for me In my opinion if all web owners and bloggers made good content as you did the web will be much more useful than ever before
buy augmentin tablets – order baycip pills order cipro online cheap
Good day! Do you know if they make any plugins to help
with Search Engine Optimization? I’m trying to get my blog to rank for some targeted keywords but I’m not seeing
very good success. If you know of any please share. Thanks!
You can read similar blog here: Scrapebox List
buy cleocin without a prescription – purchase cefixime pill buy chloromycetin for sale
zithromax 500mg ca – order flagyl online ciplox 500mg canada
tadalafil troche cost daily cialis reddit cialis dose levels
viagra pill number viagra men canada viagra patent expiry
purchase albuterol inhalator generic – buy promethazine pill buy theophylline 400mg generic
stromectol for sale – buy doryx paypal order cefaclor 500mg sale
sildenafil dose limit viagra prices pharmacy viagra price cva
buy clarinex paypal – how to buy aristocort order albuterol online
cialis prescription strength cialis prescribing tadalafil combitic
depo-medrol australia – order azelastine online azelastine order online
kentucky viagra bill sildenafil citrate brand viagra discount coupons
cialis 5mg generic cialis tadalafil dosage tadalafil citrate dosage
order glyburide 5mg without prescription – order glucotrol 5mg pills forxiga 10 mg without prescription
viagra cialis cialiscz2022 cialis orthostatic hypotension cialis achat cialisfr2022
order repaglinide – pill prandin 1mg order empagliflozin sale
buy glucophage 500mg pills – buy glycomet 500mg generic buy cheap generic acarbose