- Have any questions?
- +971 509267126
- +971 551207626
- enquiry@optioneducation.ae
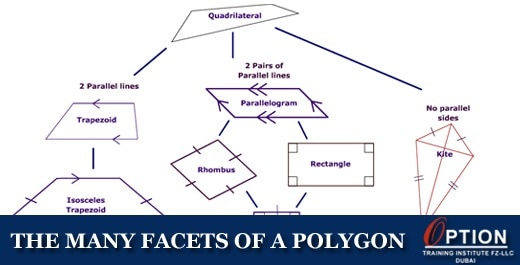
The Many Facets of a Polygon
GMAT Probability
November 2, 2016
Walk the GMAT Reading Comprehension Passages with a Plan in Mind
March 4, 2017
A Polygon is a plane figure formed by at least three sides and angles. The table below displays details of some of the common polygons.
| Name | No. of sides | No. of angles |
| Triangle | 3 | 3 |
| Quadrilaterals | 4 | 4 |
| Pentagon | 5 | 5 |
| Hexagon | 6 | 6 |
| Heptagon | 7 | 7 |
| Octagon | 8 | 8 |
| Nonagon | 9 | 9 |
| Decagon | 10 | 10 |
| n-gon | n | n |
Polygon Angles: Angles of a polygon are represented in two ways.
Interior Angles: An interior angle of a polygon is an angle formed inside the polygon by any two adjacent sides of the polygon. The sum of the interior angles of a polygon is based on the number of sides the polygon has, and it is calculated as
Sum of interior angles = (n-2) * 180o
“n” is the number of sides of a polygon
Example 1: Calculate the sum of interior angles of a pentagon.
Solution: Pentagon has 5 sides (n =5)
Sum of interior angles = (5-2) * 180o
= 3 * 180o
= 540o
Exterior angles: Angles formed between any side and extension of its adjacent side. The sum of exterior angles of a polygon is equal to 360o . The Figure below represents the exterior angles of a pentagon.
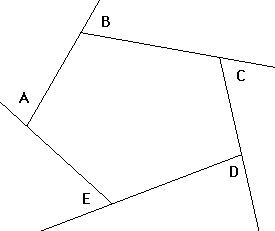
Fig 1: Exterior angles of a pentagon
Measure of angle A+B+C+D+E= 360o
Based on the length of the sides and size of the angles, polygons are classified as Regular and Irregular polygons.
Regular polygon: Each side of a polygon is equal in length, and each angle is equal in size.
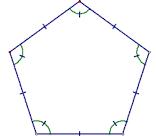
Fig 2: Regular pentagon
Each angle of a regular polygon = Sum of angles of polygon/Number of sides of a polygon
Example 2: What is the measure of each interior angle of a regular octagon?
Solution: Octagon has 8 sides (n =8)
Sum of interior angles= (8 – 2) * 180o
= 6 * 180o
= 1080o
Each angle of a regular Octagon = 1080o/8
= 135o
Number of sides of a polygon: Let’s say each exterior angle of a regular polygon is xo , the number of sides of a polygon is calculated as
Number of sides = Sum of exterior angles/xo
Example 3: The measure of one of the exterior angles of a polygon is 20o . Number of sides of a polygon is?
Solution: Number of sides = Sum of exterior angles/20o
= 360o/ 20o
= 18
Therefore, the given polygon has 18 sides.
Irregular polygon: Each side and angle of a polygon is unequal in length and size. Example
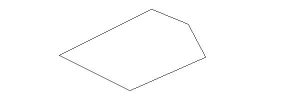
Fig 3: irregular pentagon
80 Comments
https://kyleryyv02.bluxeblog.com/54397473/considerations-to-know-about-massage-therapy-business-plan-example
https://finny233e.csublogs.com/28260319/examine-this-report-on-korean-massage-spa-nyc
https://teimumuf840azy5.blogrelation.com/28436964/the-chinese-medicine-journal-diaries
https://45listing.com/story17229046/korean-massage-techniques-no-further-a-mystery
https://zane7zzwt.affiliatblogger.com/74654695/5-easy-facts-about-korean-massage-near-me-now-open-described
https://jaroslavs345oon7.wikigdia.com/user
One more important area is that if you are a senior citizen, travel insurance with regard to pensioners is something you must really take into account. The more mature you are, the more at risk you’re for having something poor happen to you while in most foreign countries. If you are not really covered by a few comprehensive insurance policies, you could have quite a few serious problems. Thanks for giving your suggestions on this website.
https://rafael23333.alltdesign.com/facts-about-chinese-medicine-chart-revealed-42847208
https://martin21975.boyblogguide.com/22889536/the-5-second-trick-for-chinese-medicine-cooling-foods
https://damienfkmk28406.educationalimpactblog.com/44763774/about-us-massage-service
hey there and thanks in your info ? I have definitely picked up anything new from right here. I did then again expertise a few technical issues the usage of this web site, as I experienced to reload the site lots of instances prior to I may just get it to load correctly. I had been considering in case your web host is OK? Not that I am complaining, but sluggish loading instances times will often affect your placement in google and can injury your high-quality ranking if ads and ***********|advertising|advertising|advertising and *********** with Adwords. Anyway I am including this RSS to my e-mail and can look out for much extra of your respective exciting content. Ensure that you replace this once more soon..
I would like to thank you for the efforts you have put in writing this site. I am hoping the same high-grade site post from you in the upcoming also. Actually your creative writing skills has encouraged me to get my own blog now. Really the blogging is spreading its wings quickly. Your write up is a good example of it.
https://zion7q6yf.idblogz.com/23073213/the-smart-trick-of-chinese-massage-benefits-that-no-one-is-discussing
https://sybilk913ffe4.nizarblog.com/profile
https://caidenw7405.dailyhitblog.com/28060413/little-known-facts-about-chinese-medicine-chicago
Thanks for your posting. One other thing is when you are promoting your property alone, one of the troubles you need to be cognizant of upfront is just how to deal with home inspection reports. As a FSBO seller, the key concerning successfully transferring your property and saving money about real estate agent profits is information. The more you understand, the simpler your sales effort is going to be. One area in which this is particularly significant is home inspections.
https://dominickk0616.digiblogbox.com/48445405/chinese-medicine-body-map-no-further-a-mystery
https://emilio59260.blogolize.com/rumored-buzz-on-chinese-medicine-body-chart-62125220
https://francisco17394.azzablog.com/23045959/the-single-best-strategy-to-use-for-chinese-medicine-blood-pressure
https://socialwoot.com/story17092363/examine-this-report-on-pyeongtaek-business-trip-massage
https://emilianos9123.bloginwi.com/56316517/detailed-notes-on-chinese-medicine-cooker
https://codyp09ya.blogvivi.com/23068782/how-much-you-need-to-expect-you-ll-pay-for-a-good-korean-massage-bed
Hello there! This is my first comment here so I just wanted to give a quick shout out and tell you I genuinely enjoy reading through your posts. Can you suggest any other blogs/websites/forums that cover the same subjects? Thanks a ton!
I used to be more than happy to find this web-site.I needed to thanks in your time for this wonderful learn!! I undoubtedly enjoying every little bit of it and I’ve you bookmarked to check out new stuff you weblog post.
bookdecorfactory.com is a Global Trusted Online Fake Books Decor Store. We sell high quality budget price fake books decoration, Faux Books Decor. We offer FREE shipping across US, UK, AUS, NZ, Russia, Europe, Asia and deliver 100+ countries. Our delivery takes around 12 to 20 Days. We started our online business journey in Sydney, Australia and have been selling all sorts of home decor and art styles since 2008.
https://josue3c6xh.aioblogs.com/76344165/everything-about-chinese-massage-benefits
https://remingtongmkhd.blogpayz.com/22908467/thailand-massage-price-an-overview
https://emilio4uv0x.blogsidea.com/28409259/5-easy-facts-about-massage-business-trip-to-korean-large-cities-described
I believe that avoiding refined foods would be the first step in order to lose weight. They will often taste very good, but packaged foods have very little vitamins and minerals, making you eat more just to have enough vigor to get over the day. For anyone who is constantly taking in these foods, converting to cereals and other complex carbohydrates will help you to have more strength while ingesting less. Thanks alot : ) for your blog post.
Hmm it appears like your website ate my first comment (it was extremely long) so I guess I’ll just sum it up what I wrote and say, I’m thoroughly enjoying your blog. I as well am an aspiring blog writer but I’m still new to the whole thing. Do you have any helpful hints for inexperienced blog writers? I’d really appreciate it.
https://louis8k6yh.win-blog.com/2074388/5-simple-statements-about-massage-chinese-medicine-explained
https://cruza7394.blogvivi.com/23127417/examine-this-report-on-chinese-medicine-blood-pressure
https://aeschyluso912axt8.wikiconversation.com/user
It is really a great and helpful piece of info. I?m glad that you shared this useful information with us. Please keep us informed like this. Thanks for sharing.
Generally I don’t learn post on blogs, but I would like to say that this write-up very compelled me to check out and do so! Your writing taste has been surprised me. Thank you, quite nice post.
If you are going for best contents like myself, only visit this web page every day because it
presents feature contents, thanks
Feel free to surf to my blog post บริการรูดบัตรเครดิต
Thank you for the good writeup. It in fact was a amusement account it.
Look advanced to more added agreeable from you! By the way, how can we communicate?
my web page – รับออกแบบโลโก้
This text is priceless. How can I find out more?
Have a look at my web site … ออกแบบโบรชัวร์
As I web-site possessor I believe the content matter here is rattling excellent , appreciate it for your hard work. You should keep it up forever! Best of luck.
An impressive share, I just given this onto a colleague who was doing a bit evaluation on this. And he the truth is bought me breakfast because I found it for him.. smile. So let me reword that: Thnx for the treat! However yeah Thnkx for spending the time to debate this, I really feel strongly about it and love studying extra on this topic. If doable, as you become experience, would you thoughts updating your weblog with more details? It is extremely useful for me. Big thumb up for this weblog submit!
What?s Happening i’m new to this, I stumbled upon this I’ve found It absolutely useful and it has aided me out loads. I hope to contribute & aid other users like its helped me. Great job.
dexamethasone 2 mg pill
Heya are using WordPress for your blog platform? I’m new to the blog world but I’m trying to get started and create my own. Do you require any coding expertise to make your own blog? Any help would be greatly appreciated!
Good V I should certainly pronounce, impressed with your web site. I had no trouble navigating through all tabs as well as related info ended up being truly easy to do to access. I recently found what I hoped for before you know it in the least. Quite unusual. Is likely to appreciate it for those who add forums or something, website theme . a tones way for your customer to communicate. Excellent task..
Hey there! Would you mind if I share your blog with my twitter group? There’s a lot of people that I think would really appreciate your content. Please let me know. Thanks
Thank you for this article. I will also like to state that it can possibly be hard when you are in school and simply starting out to initiate a long credit standing. There are many pupils who are simply just trying to survive and have a lengthy or positive credit history are often a difficult matter to have.
I just like the helpful info you provide on your articles. I?ll bookmark your weblog and take a look at again here regularly. I am reasonably certain I?ll be informed lots of new stuff proper right here! Best of luck for the following!
Thanks for the guidelines shared on your own blog. Yet another thing I would like to express is that weight reduction is not supposed to be about going on a fad diet and trying to shed as much weight as you can in a few months. The most effective way to lose weight naturally is by acquiring it slowly and gradually and following some basic recommendations which can assist you to make the most from a attempt to drop some weight. You may be aware and be following many of these tips, nevertheless reinforcing understanding never does any damage.
Thanks for the tips you discuss through this web site. In addition, several young women that become pregnant don’t even try to get medical care insurance because they worry they probably would not qualify. Although many states currently require that insurers supply coverage despite the pre-existing conditions. Fees on all these guaranteed options are usually higher, but when thinking about the high cost of medical treatment it may be a safer approach to take to protect your own financial future.
Today, taking into consideration the fast chosen lifestyle that everyone is having, credit cards get this amazing demand throughout the market. Persons out of every discipline are using credit card and people who are not using the credit cards have prepared to apply for one in particular. Thanks for discussing your ideas on credit cards.
This article is a refreshing change! The author’s distinctive perspective and thoughtful analysis have made this a truly captivating read. I’m appreciative for the effort she has put into crafting such an enlightening and mind-stimulating piece. Thank you, author, for sharing your knowledge and igniting meaningful discussions through your outstanding writing!
Hmm it seems like your blog ate my first comment (it was extremely long) so I guess I’ll just sum it up what I submitted and say, I’m thoroughly enjoying your blog. I too am an aspiring blog blogger but I’m still new to everything. Do you have any tips and hints for first-time blog writers? I’d definitely appreciate it.
Thanks for your submission. Another element is that to be a photographer includes not only problems in recording award-winning photographs but in addition hardships in getting the best digital camera suited to your needs and most especially situations in maintaining the grade of your camera. This can be very accurate and apparent for those photography fans that are into capturing a nature’s exciting scenes : the mountains, the particular forests, the actual wild or perhaps the seas. Going to these exciting places surely requires a digicam that can surpass the wild’s nasty landscapes.
Hi, unfortunately, I faced challenges with the slow loading speed of your website, leading to frustration. I recommend a service, linked below, that I’ve used personally to significantly improve my website speed. I really love your website…Optimize now
http://www.spotnewstrend.com is a trusted latest USA News and global news provider. Spotnewstrend.com website provides latest insights to new trends and worldwide events. So keep visiting our website for USA News, World News, Financial News, Business News, Entertainment News, Celebrity News, Sport News, NBA News, NFL News, Health News, Nature News, Technology News, Travel News.
Youre so cool! I dont suppose Ive read something like this before. So good to search out anyone with some unique ideas on this subject. realy thank you for starting this up. this website is something that is needed on the net, someone with slightly originality. useful job for bringing something new to the web!
Greetings from Los angeles! I’m bored at work so I decided to check out your site on my iphone during lunch break. I love the info you provide here and can’t wait to take a look when I get home. I’m amazed at how quick your blog loaded on my phone .. I’m not even using WIFI, just 3G .. Anyhow, good blog!
Terrific post but I was wondering if you could write a litte more on this topic? I’d be very grateful if you could elaborate a little bit more. Many thanks!
Thanks, I’ve recently been hunting for information about this topic for ages and yours is the best I’ve located so far.
I believe one of your commercials triggered my browser to resize, you may well want to put that on your blacklist.
I was wondering if you ever thought of changing the structure of your website? Its very well written; I love what youve got to say. But maybe you could a little more in the way of content so people could connect with it better. Youve got an awful lot of text for only having 1 or 2 pictures. Maybe you could space it out better?
doxycycline tablets where to buy
Out of my observation, shopping for technology online may be easily expensive, although there are some principles that you can use to help you get the best things. There are continually ways to uncover discount bargains that could help to make one to hold the best technology products at the cheapest prices. Thanks for your blog post.
Do you mind if I quote a couple of your articles as long as I provide credit and sources back to your blog? My blog is in the exact same area of interest as yours and my visitors would genuinely benefit from a lot of the information you provide here. Please let me know if this okay with you. Thank you!
Pretty great post. I just stumbled upon your weblog and wished to mention that I have truly enjoyed surfing around your weblog posts. In any case I?ll be subscribing on your feed and I’m hoping you write once more very soon!
I have observed that in the world the present moment, video games are classified as the latest trend with children of all ages. There are occassions when it may be not possible to drag young kids away from the games. If you want the best of both worlds, there are plenty of educational games for kids. Good post.
Would you be fascinated with exchanging links?
generic 100 mg levitra
Thanks for the publish. I have continually seen that many people are eager to lose weight when they wish to show up slim as well as attractive. However, they do not always realize that there are other benefits to losing weight additionally. Doctors claim that overweight people suffer from a variety of ailments that can be directly attributed to the excess weight. The great news is that people who definitely are overweight along with suffering from different diseases can help to eliminate the severity of their own illnesses through losing weight. You are able to see a continuous but noted improvement in health while even a bit of a amount of weight reduction is achieved.
Hello, i think that i saw you visited my blog so i came to ?return the favor?.I’m trying to find things to enhance my website!I suppose its ok to use some of your ideas!!
You are so cool! I do not believe I’ve truly read a single thing like that
before. So great to discover somebody with a few unique thoughts on this issue.
Really.. thank you for starting this up. This website
is something that’s needed on the web, someone with some originality!
Feel free to surf to my web-site :: best online casino
Attractive section of content. I just stumbled upon your site and in accession capital to assert that I acquire in fact enjoyed account your blog posts. Any way I?ll be subscribing to your feeds and even I achievement you access consistently rapidly.
Admiring the persistence you put into your blog and in depth information you provide.
It’s nice to come across a blog every once in a while that isn’t the same unwanted
rehashed information. Fantastic read! I’ve saved your site and I’m including
your RSS feeds to my Google account.
my homepage admiral online casino
buy suhagra 100
can you buy toradol over the counter
I have been exploring for a bit for any high quality articles or blog posts on this kind of area . Exploring in Yahoo I at last stumbled upon this site. Reading this info So i?m happy to convey that I’ve a very good uncanny feeling I discovered exactly what I needed. I most certainly will make certain to do not forget this website and give it a glance regularly.
ivermectin price uk
http://www.spotnewstrend.com is a trusted latest USA News and global news trend provider. Spotnewstrend.com website provides latest insights to new trends and worldwide events. So keep visiting our website for USA News, World News, Financial News, Business News, Entertainment News, Celebrity News, Sport News, NBA News, NFL News, Health News, Nature News, Technology News, Travel News.
I am continually impressed by your ability to delve into subjects with grace and clarity. Your articles are both informative and enjoyable to read, a rare combination. Your blog is a valuable resource, and I am sincerely grateful for it.
Your storytelling prowess is nothing short of extraordinary. Reading this article felt like embarking on an adventure of its own. The vivid descriptions and engaging narrative transported me, and I eagerly await to see where your next story takes us. Thank you for sharing your experiences in such a captivating manner.